25 ++ tan^-1(2x/1-x^2) formula 359185-Tan inverse 2x/1-x^2 formula

{eq}\int\frac{2x^2 1}{ (2x 1)(x^2 1)} dx {/eq} Partial Fraction Decomposition Method An integral is solved using the partial fraction decomposition method (if possible) if it contains aAlgebra Factoring Formula Product Formula Power Formula Logarithm Formula Equation and Solutions Inequalities Compound Interest Formula Root Formula Trigonometry 1 For the question, tan(2x)tanx = 1, I divided it by tanx, and got the solution as ( 2n 1) π 6 tan2x = cotx = tan(π 2 − x) So, 2x = nπ π 2 − x So, 3x = ( 2n 1) π 2 But the book solved using the formula of tan(2x), and got the solution as ( 6n ± 1) π 6 I can see that my solution has odd multiples of π / 2, which should be

Integration Of Tan Inverse X Ex 7 6 13 Chapter 7 Class 12

Tan inverse 2x/1-x^2 formula

Tan inverse 2x/1-x^2 formula-Before reading this, make sure you are familiar with inverse trigonometric functions The following inverse trigonometric identities give an angle in different ratios Before the more complicated identities come some seemingly obvious ones Be observant of the conditions the identities call for sin ⁡ − 1 ( − x) = − sin ⁡ − 1 x, ∣Click here👆to get an answer to your question ️ Prove that 2tan^1x = tan^1 2x1 x^2

Example 3 Show I Sin 1 2x Root 1 X2 2 Sin 1 X Examples

`tan^( 1)xtan^( 1)\ (2x)/(1x^2)=pitan^( 1)\ (3xx^3)/(13x^2),(x >0)` সত্য যদি Bihar Inter Results 21 BSEB has released class 12mark sheets, Students canAnswer ∫ tan 1 x dx = x tan 1 x ½ ln (1x 2 ) C We will use the product rule formula to find the int tan 1 x dx So, now we need to integrate tan 1 x Now to evaluate integration of tan 1 x, let u = tan 1For each of the three trigonometric substitutions above we will verify that we can ignore the absolute value in each case when encountering a radical 🔗 For x = asinθ, x = a sin ⁡ θ, the expression √a2 −x2 a 2 − x 2 becomes √a2−x2 = √a2−a2sin2θ= √a2(1−sin2θ)= a√cos2θ= acosθ = acosθ a 2 − x 2 = a 2 − a 2

Let P = a i j be a 3 × 3 matrix and let Q = b i j where b i j = 2 i j a i j for 1 ≤ i, j ≤ If the determinant of P is 2, then the determinant of the matrix Q is 5 If the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is Prove that tan^1x tan^1(2x/(1 x^2)) = tan^1((3x x^3)/(1 3x^2)) asked in Trigonometry by KumkumBharti ( 539k points) inverse trigonometric functions Solve for `x` `tan^(1)(2x)/(1x^(2))cot^(1)(1x^(2))/(2x))=pi/3, 1 lt x lt 1`

INVERSE TRIGONOMETRIC FUNCTIONS 23 Therefore, tan(cos–1x) = 1–cos θ 21– tanθ = cosθ x x = Hence 2 –1 8 1– 8 17 15 tan cos = 17 8 8 17 = Example 11 Find the value of –1 –5 Inverse Trigonometric Formulas Trigonometry is a part of geometry, where we learn about the relationships between angles and sides of a rightangled triangleIn Class 11 and 12 Maths syllabus, you will come across a list of trigonometry formulas, based on the functions and ratios such as, sin, cos and tanSimilarly, we have learned about inverse trigonometry concepts alsoAnswer with step by step detailed solutions to question from HashLearn's Math CPPs (JEE), Integral Calculus "integral 2x1/( x1 )(x^21 ) dx" plus more questions from Mathematics Questions of this type are frequently asked in competitive entrance

Solve For X Tan 1 2x 1 X 2 Cot 1 1 X 2 2x Pi 3 1ltxlt1

Notes On A Level P3 Integration Notes

Two numbers r and s sum up to 2 exactly when the average of the two numbers is \frac{1}{2}*2 = 1 You can also see that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxC 3 Derivatives of the Inverse Trigonometric Functions by M Bourne Recall from when we first met inverse trigonometric functions " sin1 x" means "find the angle whose sine equals x" Example 1 If x = sin1 025 then by using the calculator, x = 15° We have found the angle whose sine is 025 Solution Let x = sec θ, then x 2 − 1 = s e c 2 θ − 1 = tan θ Therefore, cot–1= 1 x 2 – 1 = cot–1 (cot θ) = θ = sec–1 x, which is the simplest form Inverse trigonometric formula here deals with all the essential trigonometric inverse function which will make it easy for you to learn anywhere and anytime ITF formula for class

Int Tan 1 2x 1 X 2 Dx

Evaluate Inttan 1 X Dx

Tan 1 (2x/ (1x 2 )=2tan 1 x cot 1 ( (1x 2 )/2x 2 )=tan 1 (2x 2 / (1x 2 )) use the formula tan 1 a tan 1 b =tan 1 ( (ab)/ (1ab)) Approved ankit dewangan 32 Points 9 years ago now i have only days to my board exams suggest some tricks solve for x tan inverse(2x/1x^2) cot inverse (1x^2/2x)= pi/3, 1Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

Derivatives Of Inverse Functions Ppt Download

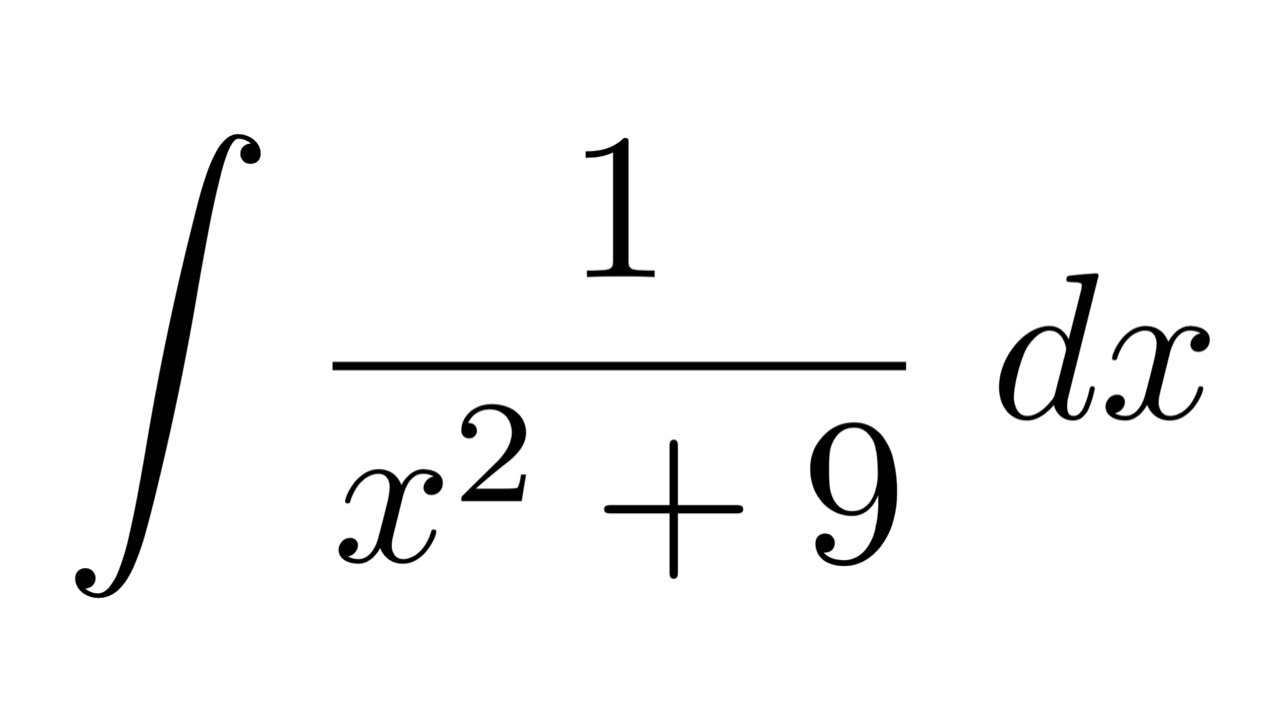
Integral Of 1 X 2 9 Substitution Youtube

Tan^1 x Not sure if you mean arctan x or (tan x)^1 which is cot x (i) y = arctan x Then, tan y = x Differentiating implicitly wrt x sec^2 y 1 dy/dx = 1 sec^2 y dy/dx = 1 dy/dx = 1/sec^2 y And, tan y = x , so, tan^2 y = x^2 sec^2 y = 1Cos Inverse 1 X 2 1 X 2 Formula Solve For X Cos 1 X 2 1 X 2 1 1 2tan 1 2x 1 X 2 2pi 3 Youtube For more information and source, see on this link https Solve For X Tan 1 2x 1 X 2 Cot 1 1 X 2 2x P 3 1 X 1 Sarthaks Econnect Largest Online Education CommunityIntegral of tan^2 (x) \square!

3

Www Amherst Edu Media View Original Ma11spring10finalanswers Pdf

Whole number n if $sin\ θ=sin\ a,$ then $θ=nπ(1)^n\ a$ if $cosec\ θ=cosec\ a,$ then $θ=nπ(1)^n\ a$ if $cos\ θ=cos\ a,$ then $θ=2nπ±a$ if $sec\ θ=secUse the distributive property to multiply y by x 2 1 Add x to both sides Add x to both sides All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtractionThis means ∫π 0 sin(x)dx= (−cos(π))−(−cos(0)) =2 ∫ 0 π sin ( x) d x = ( − c o s ( π)) − ( − c o s ( 0)) = 2 Sometimes an approximation to a definite integral is desired A common way to do so is to place thin rectangles under the curve and add the signed areas together WolframAlpha can solve a broad range of integrals

Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12

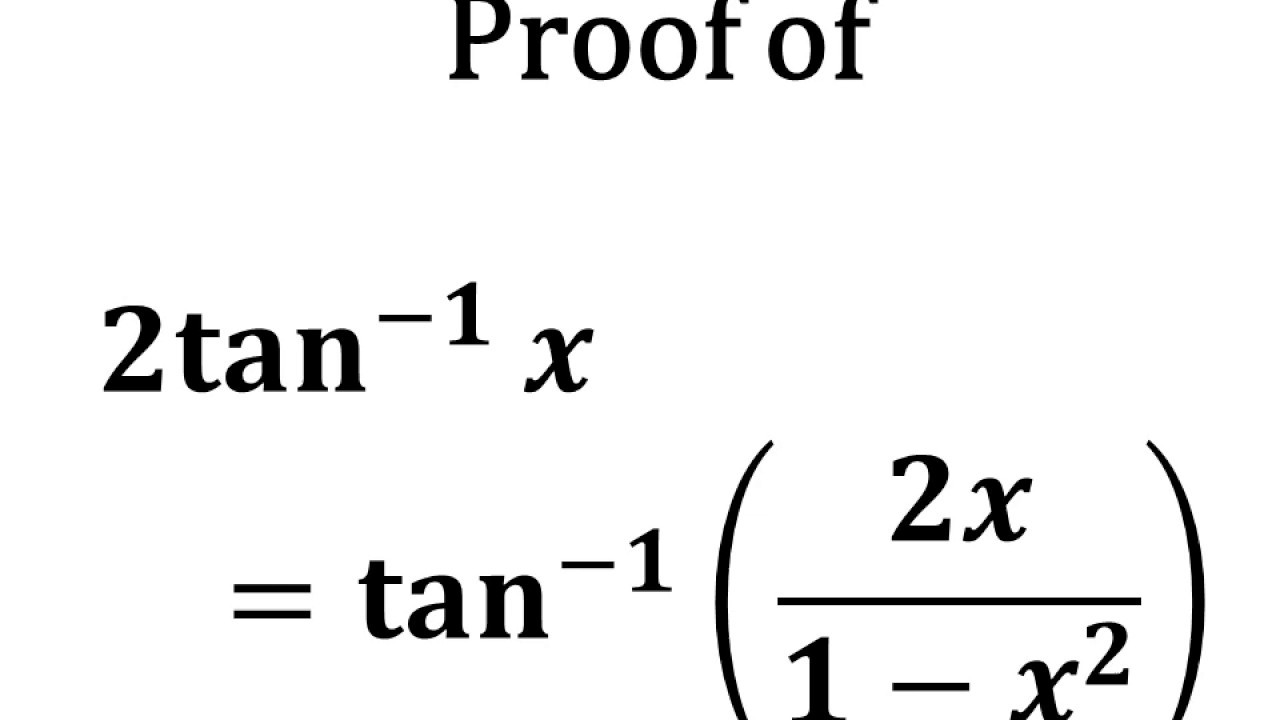
2tan 1 X Tan 1 2x 1 X 2 2arctan X Arctan 2x 1 X 2 Youtube

Differentiate wrtx du/dx = 2/ (1 x 2) Let v = sin 1 2x/ (1x 2) Put x = tan θ So v = sin 1 2 tan θ/ (1 tan 2 θ) = sin 1 sin 2θ = 2θ = 2 tan 1 x dv/dx = 2/ (1 x 2)Solve the following equations for x 2 tan^1(sin x) = tan^1 (2 sec x), x ≠ π/2 asked Apr 2 in Trigonometry by Takshii ( 346k points) inverse trigonometric functionsSolve the Following Equation For X `Tan^1 X/2Tan^1 X/3=Pi/4, 0

Ex 2 2 5 Simplify Tan 1 Root 1 X2 1 X Chapter 2

Tan 1 3 2x 1 6x Differentiate W R T X

Limit Calculator Step 1 Enter the limit you want to find into the editor or submit the example problem The Limit Calculator supports find a limit as x approaches any number including infinity The calculator will use the best method available so try out a lot of different types of problems You can also get a better visual and understandingSolve for x tan^1 (x 1) tan^1 x tan^1 (x 1) = tan^1 3xTan1 x = Cot1 1/x Formula 3 The sum of the complementary inverse trigonometric functions results in a right angle For the same values of x, the complementary functions have complementary angles as answers, and the sum of it is equal to a right angle Sin1 x Cos1 x = π/2 Tan1 x Cot1 x = π/2 Sec1 x Cosec1 x = π/2 Formula 4

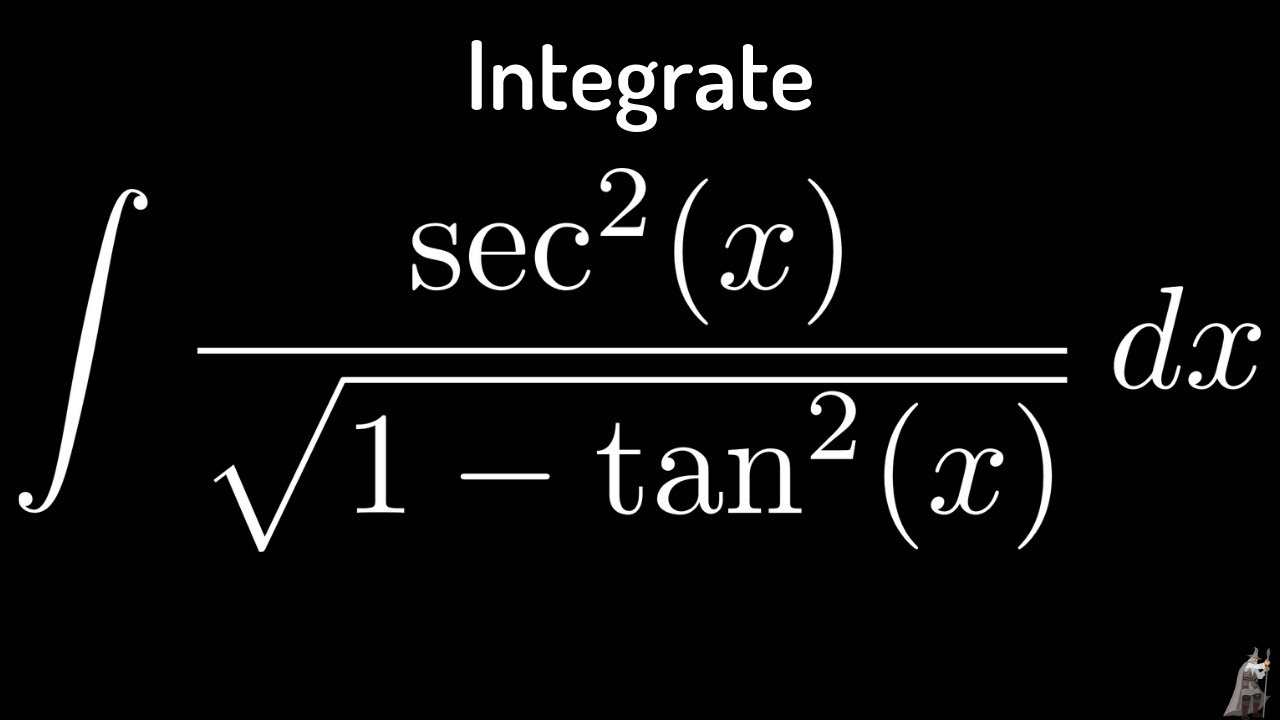
Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube

Ex 7 10 3 Evaluate Integrals Sin 1 2x 1 X2 Dx Ex 7 10

Use of Integration by Parts Calculator For the integration by parts formula, we can use a calculator The steps to use the calculator is as follows Step 1 Start by entering the function in the input field Step 2 Next, click on the "Evaluate the Integral" button to get the output Step 3 The integrated value will be displayed in theNotation Several notations for the inverse trigonometric functions exist The most common convention is to name inverse trigonometric functions using an arc prefix arcsin(x), arccos(x), arctan(x), etc (This convention is used throughout this article) This notation arises from the following geometric relationships citation needed when measuring in radians, an angle of θThen by using the formula used for solving functions in parametric form ie Lastly substituting the values of du/dx and dv/dx and simplify to obtain the result Calculation Let u = tan1 x and v = cot1 x Differentiating with respect to x, we get \(\rm \frac{du}{dx} = \frac{d(\tan^{1

Misc 14 Solve Tan 1 1 X 1 X 1 2 Tan 1 X Ncert

Solve The Equation 2 Tan 1 2x 1 Cos 1 X

The other answer so far (from Eshaan Joshe) should put you on your way, but be careful that that answer meant 1/(1x^2) If you continue taking the derivatives, you can look for a pattern (using arctan to mean tan^1) first derivative of (arctanFunction of x, not of y We must now plug in the original formula for y, which was y = tan−1 x, to get y = cos2(arctan(x)) This is a correct answer but it can be simplified tremendously We'll use some geometry to simplify it 1 x (1x2)1/2 y Figure 3 Triangle with angles and lengths corresponding to those in the exam­ pleDetailed explanation with examples on propertiesofinversetrigonometricfunctions helps you to understand easily , designed as per NCERT QnA , Notes & Videos

Derivative Of Tan Inverse With Chain Rule Youtube

Tan Inverse 2x 1 X Square Cot Inverse 1 X Square 2x 2pi 3 Brainly In

 Let me rewrite the proof a bit differently We are required to prove (RTP) that $$2\tan^{1}(y \sqrt{1y^2}) \tan^{1} (y) = \frac{\pi}{2}$$ Proof Plan We will use the formula F first, followed by the identity I Example 7 Show that tan1 𝑥 tan1 2𝑥/(1 −𝑥2) = tan1 (3𝑥 − 𝑥3)/(1 − 3𝑥2) Solving LHS tan1 𝑥 tan1 2𝑥/(1 − 𝑥2) = tan1 (𝑥The inverse trigonometric functions are also called arcus functions or anti trigonometric functions These are the inverse functions of the trigonometric functions with suitably restricted domainsSpecifically, they are the inverse functions of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric

What Is The Integration Of Log 1 X 2 Quora

Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh

The inverse function reverses this operation, taking the ratio of sides as input and returning the angle as output sin ⁡ − 1 ( b c) = θ cos ⁡ − 1 ( a c) = θ tan ⁡ − 1 ( b a) = θ = θ = θ = θ This means the inverse trigonometric functions are useful whenever weIn differential calculus, the differentiation of the sin inverse function is written in mathematical form as follows ( 1) d d x ( sin − 1 ⁡ ( x)) ( 2) d d x ( arcsin ⁡ ( x)) The differentiation of the inverse sin function with respect to x is equal to the reciprocal of the square root of the subtraction of square of x from oneThe integration of tangent inverse is of the form I = ∫ tan – 1 x d x To solve this integration, it must have at least two functions, however it has only one function tan – 1 x So, consider the second function as 1 Now the integration becomes I = ∫ tan – 1 x ⋅ 1 d x – – – ( i) The first function is tan – 1 x and the

Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6

Domain Range Of Inverse Tangent Function Video Khan Academy

 Next Integration Formula Sheet Chapter 7 Class 12 Formulas→ Chapter 7 Class 12 Integrals (Term 2) Serial order wise; #tan^1(xsqrt(1x^2))#,Express the value of the above in the simplest form?Example 1 In the integral we may write = ⁡, = ⁡, = ⁡, so that the integral becomes = ⁡ ⁡ = ⁡ ( ⁡) = ⁡ ⁡ = = = ⁡ , provided For a definite integral, the bounds change once the substitution is performed and are determined using the equation = ⁡, with values in the range <

Prove That Tan 1x Tan 1 2x1 X 2 Tan 1 3x X 31 3x 2

Ex 5 3 10 Find Dy Dx In Y Tan 1 3x X3 1 3x2 Ex 5 3

Miscellaneous Misc 1 Important Misc 2 Important Misc 3 Important Misc 4 Misc 5 Important Misc 6

First Degree Equation 2x 1 0 Lunlun Com

Example 3 Show I Sin 1 2x Root 1 X2 2 Sin 1 X Examples

Let U Sin 1 2x 1 X 2 And V Tan 1 2x 1 X 2 Then D U D V A 1 2 B X C 1 X 2 1 X 2 D 1

List Of Trigonometric Identities Wikipedia

Solve For X Tan 1 X 1 Tan 1 X 1 Tan 1 8 31 Youtube

2tan 1 X Sin 1 2x 1 X 2 2arctan X Arcsin 2x 1 X 2 Youtube

Notes On A Level P3 Integration Notes

If Tan 1 X2 Y2 X2 Y2 A Prove That Dy Dx X 1 Tana Y 1 Tana Brainly In

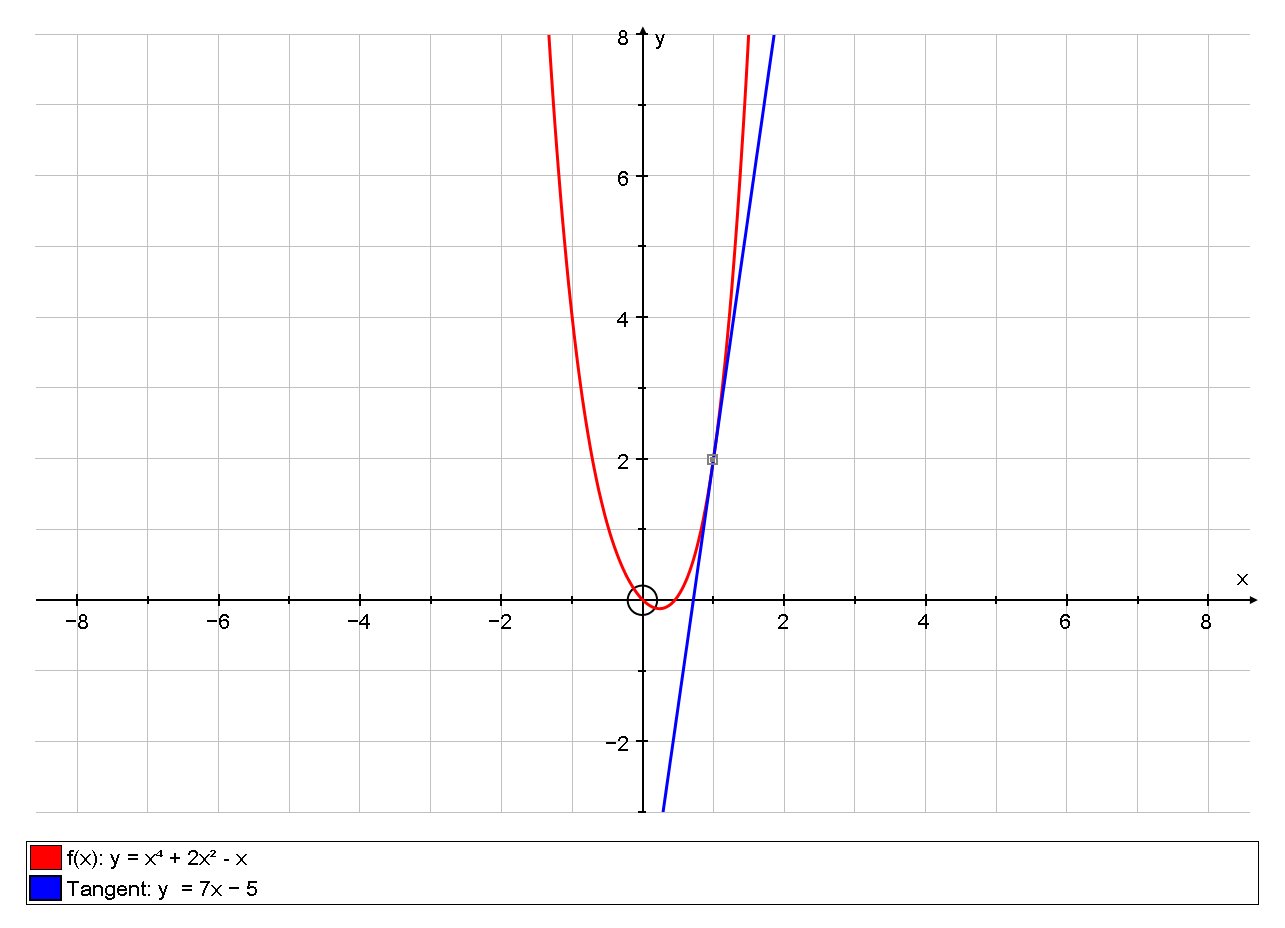
How Do You Find The Equation Of The Tangent Line To The Curve Y X 4 2x 2 X At 1 2 Socratic

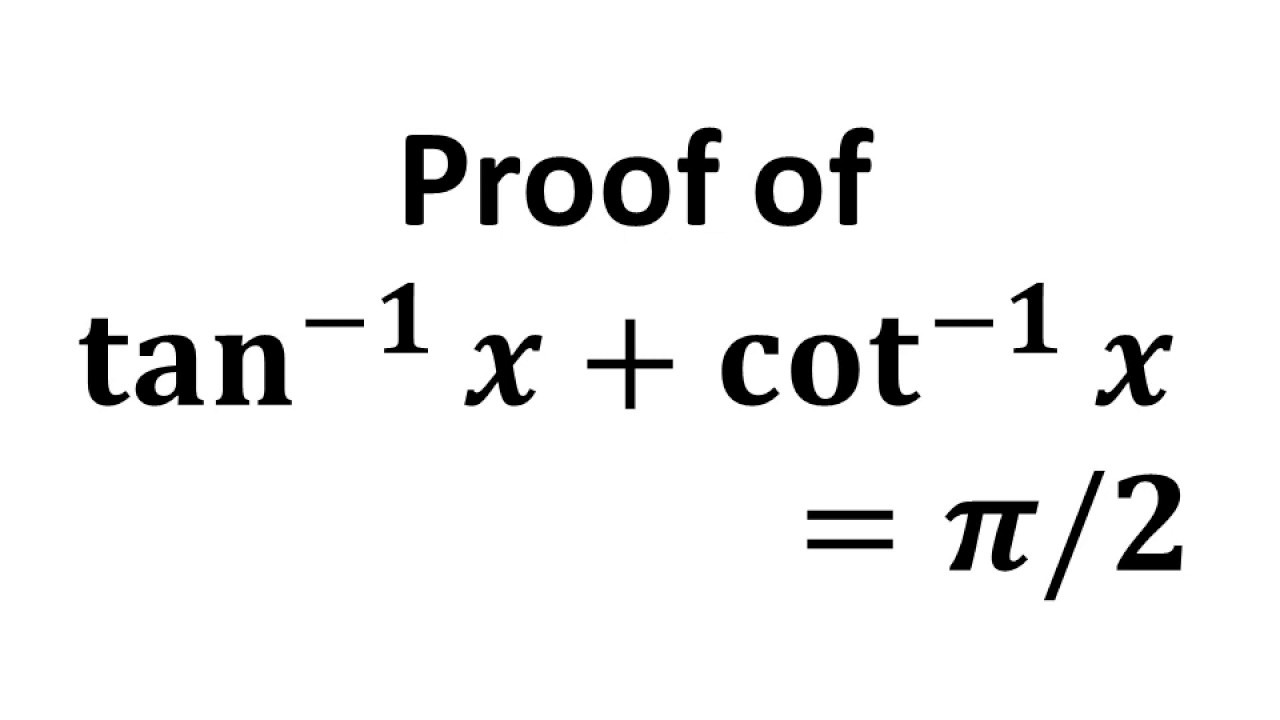
Tan 1 X Cot 1 X Pi 2 Arctan X Arccot X Pi 2 Youtube

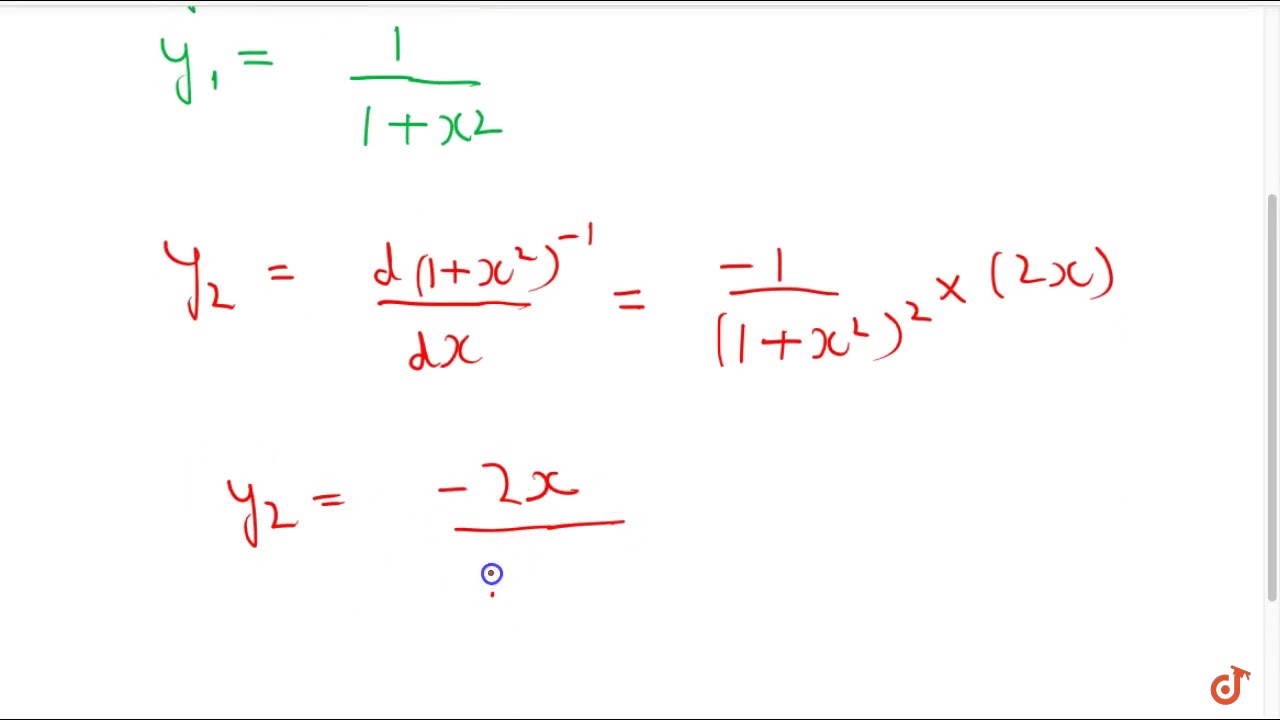
If Y Tan 1 X Show That 1 X 2 D 2y Dx 2 2x Dy Dx 0 Youtube

Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous

Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12

Worked Example Implicit Differentiation Video Khan Academy

Example 22 Find I Ex Tan 1 X 1 1 X2 Dx Examples

Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh

Example 7 Show That Tan 1 X Tan 1 2x 1 X2 Inverse

Ex 2 2 13 Inverse Trigonometry Tan 1 2 Sin 1 2x 1 X2

Derive The Following Formulas For The Inverse Chegg Com

Ex 7 11 8 Evaluate Integral 0 Pi Log 1 Tan X Teachoo

Www3 Nd Edu Apilking Math Work Old exams Exams s13 M final sp13 solution Pdf

Solve For X Cos 1 X 2 1 X 2 1 1 2tan 1 2x 1 X 2 2pi 3 Youtube

1

Differentiate Tan 1 2x 1 X 2 W R T Sin 1 2x 1 X 2

I Ff X 2tan 1 X Sin 1 2x 1 X 2 X 1 T H E N F 5 Is Equal To

Derivatives Of Inverse Functions Video Khan Academy

Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 7 Pdf

Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6

Solving The Differential Equation Dy Dx Tan 2 X Y Youtube

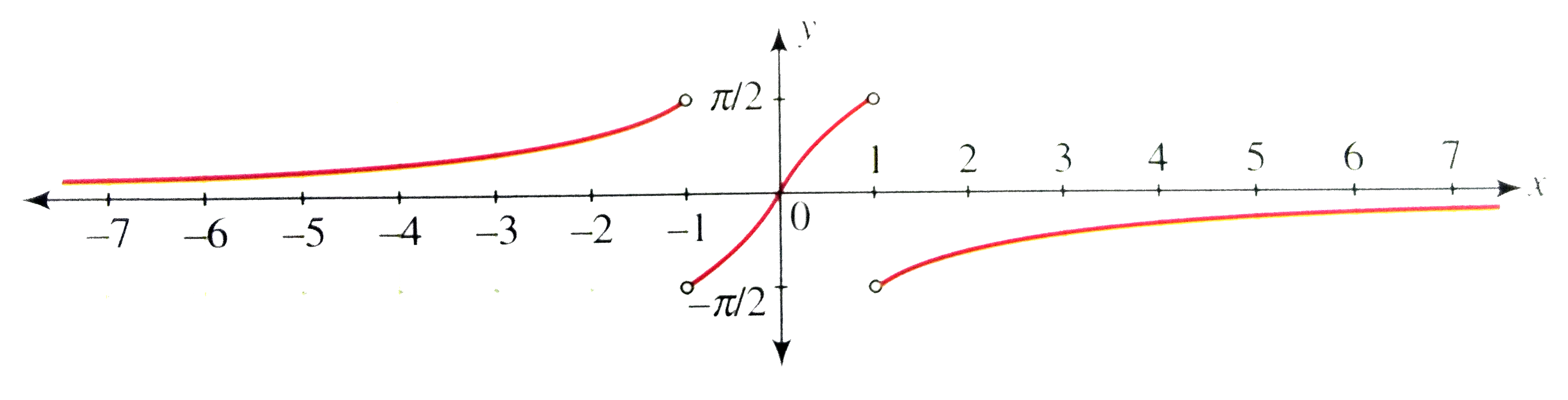
Draw The Graph Of Y Tan 1 2x 1 X 2

The Derivative Of Tan 1 2x 1 X 2 With Respect To Sin 1 2x 1 X 2 Is Youtube

Ex 2 2 9 Class 12 Inverse Cbse Tan 1 X Root X2

What Is Cos Tan 1 X Quora

Find The Value Of Tan 1 2 Sin 1 2x 1 X 2 Cos 1 1 Y 2 1 Y 2 X 1 Y 0and X Y 1

Tan 1 X Tan 1 Y Tan 1 X Y 1 Xy Arctan X Arctan Y Arctan X Y 1 Xy Youtube

Range Of Tan 1 2x 1 X 2 Is A Pi 4 Pi 4 B Pi 2 Pi 2 C Pi 2 Pi 4 D Pi 4 Pi 2

If Y 2tan 1 X Sin 1 2x 1 X 2 Then Lt Y Lt

Integration Of Tan Inverse X Ex 7 6 13 Chapter 7 Class 12

Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh

If Y Tan 1 2 X 1 2 2x 1 Then Dy Dx At X 0 Is Youtube

Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous

How Do You Find The Equations Of The Tangent Lines To The Curve Y X 1 X 1 That Are Parallel To The Line X 2y 2 Socratic

Tan 1 2x 1 15x 2

Notes On A Level P3 Integration Notes

Madasmaths Com Archive Maths Booklets Standard Topics Trigonometry Trigonometric Inverse Functions Pdf

1

Integral 1 Tan 2 X Sec 2 X Youtube

Ex 5 3 13 Find Dy Dx In Y Cos 1 2x 1 X2 Ncert Ex 5 3

Example 7 Show That Tan 1 X Tan 1 2x 1 X2 Inverse

Inverse Trigonometry Trigonometric Functions Sine

Derivatives Of Inverse Functions Ppt Download

Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6

Integration Of Tan Inverse X Ex 7 6 13 Chapter 7 Class 12

Prove That 1 2tan 1x Cos 1xsqrt 1 Sqrt 1 X 2 2sqrt 1 X 2 Youtube

Yorkshiremathstutor Com Wp Content Uploads 19 02 8 Differentiation Answers Pdf

Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6

Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12

Tan 2x Formula What Is Tan 2x Formula Examples

Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous

21 Differentiation And Integration Of Trigonometry Function 9709

1

Differentiate Tan 1 1 X 2 X With Respect To Cos 1 2x 1 X 2 When X 0

Solve Tan 1 X Tan 1 2x 1 X 2 Pi 3

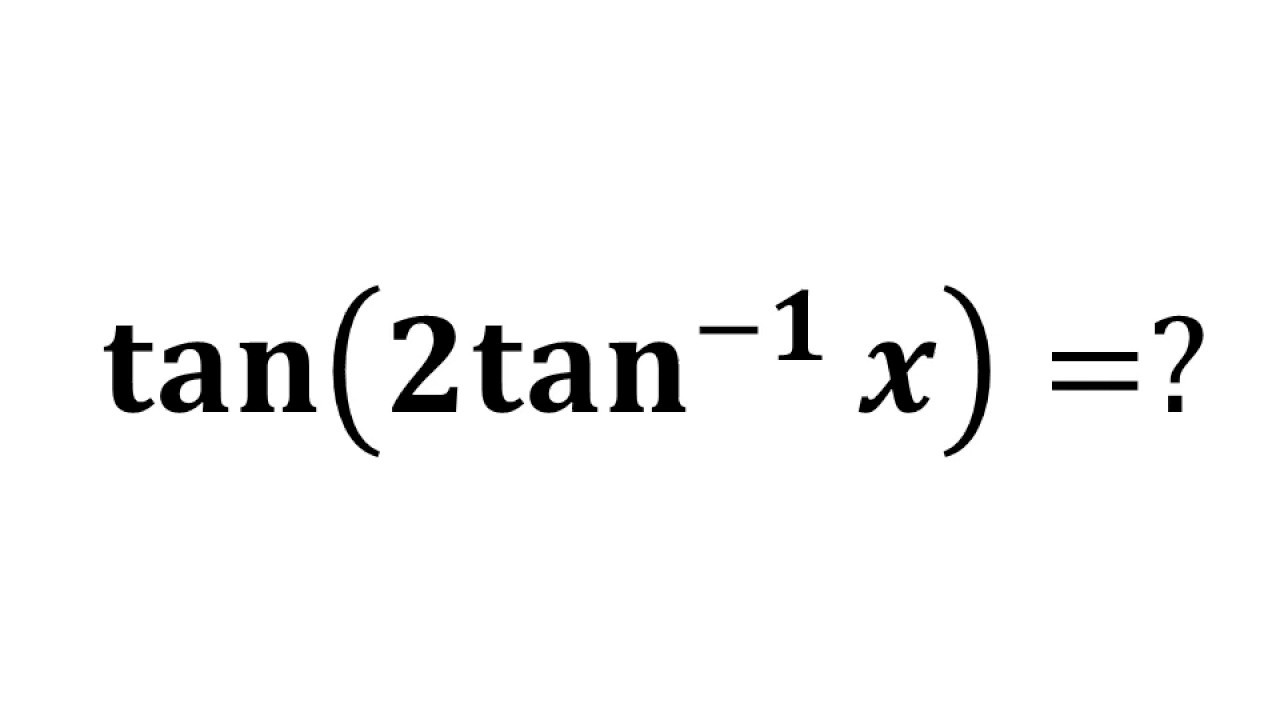
Tan 2 Tan 1 X Tan 2 Arctan X Youtube

Integration Of Inverse Tan 2x Integration By Parts Youtube

Prove That Sin 1 2x 1 X 2 2sin 1x X 1 2

Differentiate Sin 1 2x 1 X 2 W R T Tan 1 X 1 Lt X Lt 1

How To Solve Tan 1 2x 1 X2 Cot 1 1 X2 2x Pie 3 Brainly In

Let Tan 1 Y Tan 1 X Tan 1 2x 1 X 2 Where X 1 Sqrt 3 Then A Value Of Y Is 1 3x X 3 1 3x 2 2 3x X 3 1 3x 2 3 3x X 3 1 3x 2 4 3x X 3 1 3x 2

If Y Tan 1 2x 1 X 2 Then Prove That Dy Dx 2 1 X 2

Integral Of 1 1 X 2 Youtube

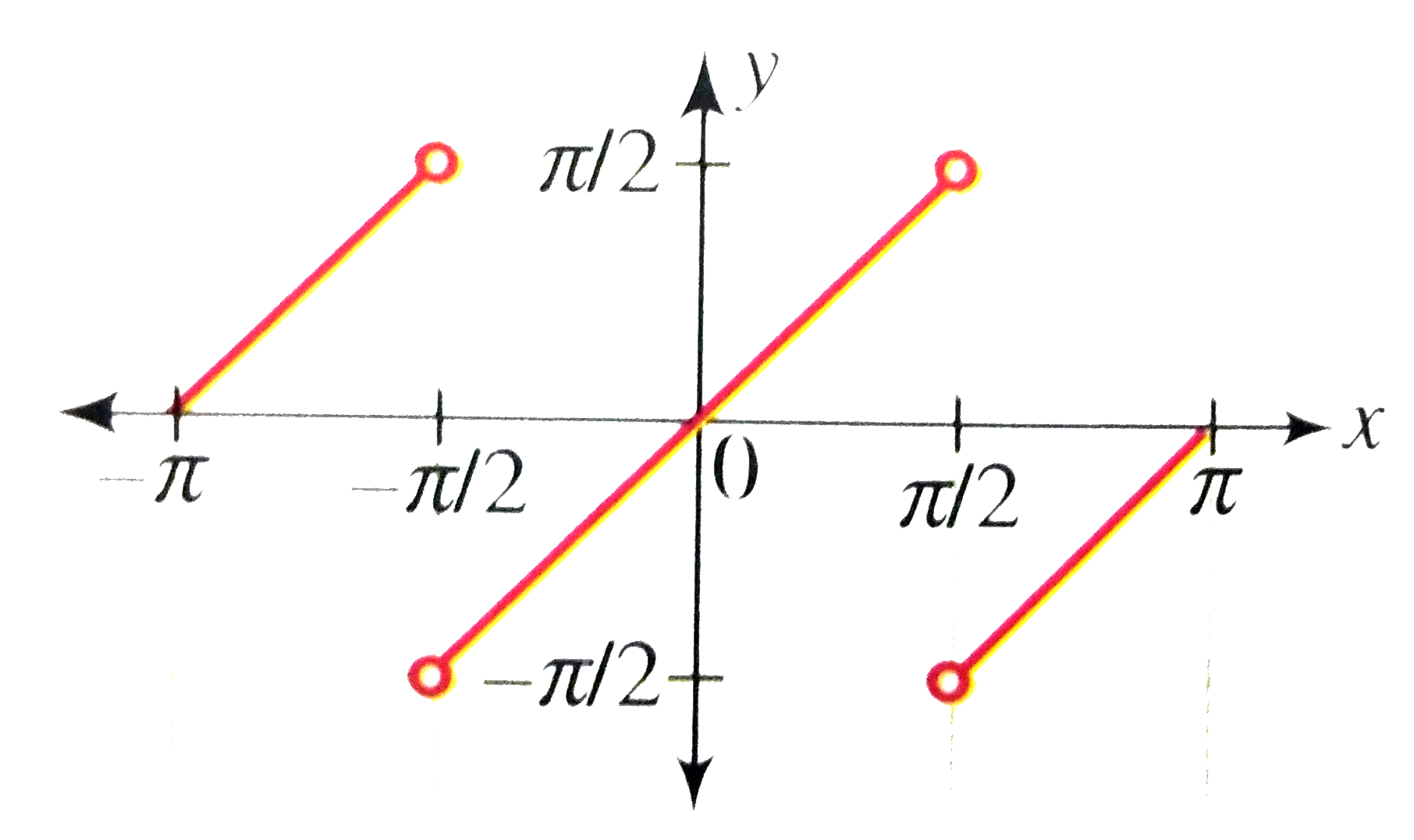
Draw The Graph Of Y Tan 1 2x 1 X 2

Differentiate Tan 1 2x 1 X 2 With Respect To Cos 1 1 X 2 1 X 2 If 0 X 1

Prove That Tan 1 X Tan 1 2x 1 X 2 Tan 1 3x X 3 1 3x 2 X Lt 1 Sqrt 3

Ex 2 2 5 Simplify Tan 1 Root 1 X2 1 X Chapter 2

Ex 2 2 4 Prove 2tan 1 1 2 Tan 1 1 7 Tan 1 31 17 Ex 2 2

Misc 13 Solve 2 Tan 1 Cos X Tan 1 2 Cosec X Miscellaneous

Notes On A Level P3 Integration Notes

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

Solve Tan 1 1 1 2x Tan 1 1 1 4x Tan 1 2 X 2

Incoming Term: tan^-1(2x/1-x^2) formula, tan inverse 2x/1-x^2 formula,